R. Alsaedi: Multiple low-energy solutions of a Neumann problem with variable exponents, p. 303-315

Abstract:

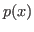
We study a class of nonhomogeneous elliptic problems with Neumann boundary condition and involving the $p(x)$-Laplace operator and power-type nonlinear terms with variable exponent. The main result of this paper establishes a sufficient condition for the existence of infinitely many weak solutions, provided that the positive parameter is sufficiently small. We also prove that these solutions are low-energy solutions, that is, they converge to zero in an appropriate function space with variable exponent. The proof combines variational arguments with a recent symmetric version of the mountain pass lemma.

Key Words: nonhomogeneous elliptic problem; variable exponent; Neumann boundary condition; mountain pass.

2010 Mathematics Subject Classification: Primary 35J60,
Secondary 58E05