Octav Olteanu: Invariant Subspaces and Invariant Balls of Bounded Linear Operators, p. 261-271

Abstract:

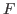
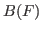
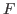
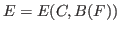
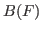
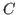
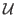
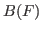
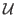
Let $F$ be a complex Banach space, $B(F)$ the algebra of all bounded operators acting on $F$, $E = E(\mathbb{C}, B(F))$ the Fréchet space of all entire functions from the complex plane into $B(F)$, endowed with the topology of uniform convergence on the compact subsets in $\mathbb{C}$. Let $\mathcal{U}$ be a subset of $B(F)$ such that the product of any two elements from $\mathcal{U}$ is still an element of $\mathcal{U}$. 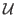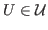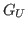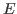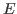For $U \in \mathcal{U}$, one denotes by $G_U$ the linear continuous operator from $E$ into $E$ defined by $(G_U f)(z) = Uf(z)$, $z \in \mathbb{C}$, $f \in E$. 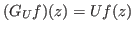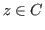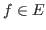One proves that there exist common invariant subspaces of all operators in $\{G_U; U \in \mathcal{U}\}$. 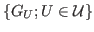In particular, there exist common invariant subspaces for all operators in $\{G_U; U \in B(F)\}$. 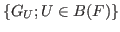One describes the elements of a dense subspace of such an invariant subspace. On the other side, a differential equation with operator - valued solution is discussed, in the Hilbert space setting. A related example is given, where an invariant subspace appears as a kernel of a differential operator. This subspace stands for a hyperinvariant subspace related to an arbitrary operator in $B(H)$. 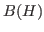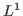Finally, the invariance of the unit ball in some $L^1$ spaces in terms of polynomials is discussed. To this end, polynomial approximation on unbounded subsets is applied.

Key Words: invariant subspace problem, invariant balls, bounded operators, sandwich type theorems for operators, approximation

2010 Mathematics Subject Classification: Primary 47A15,
Secondary 41A10, 47A63