Abstract:
We investigate the collapsibility of systolic finite simplicial
complexes of arbitrary dimension. The main tool we use in the
proof is discrete Morse theory. We shall consider a convex
subcomplex of the complex and project any simplex of the complex
onto a ball around this convex subcomplex. These projections will
induce a convenient gradient matching on the complex. Besides we
analyze the combinatorial structure of both CAT(0) and systolic
locally finite simplicial complexes of arbitrary dimensions. We
will show that both such complexes possess an arborescent
structure. Along the way we make use of certain well known results
regarding systolic geometry.
Key Words: local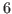 
-largeness, directed geodesic, Morse matching, collapsibility, arborescent structure
2010 Mathematics Subject Classification: Primary 05C99, Secondary 05C75
