Ralph R. Gomez: A Note On Smale Manifolds and Lorentzian Sasaki-Einstein Geometry, p.151-158

Abstract:

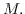
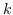
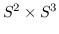
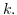
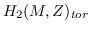
In this note, we construct new examples of Lorentzian Sasaki-Einstein (LSE) metrics on Smale manifolds $M.$ It has already been established by the author that such metrics exist on the so-called torsion free Smale manifolds, i.e. the $k$-fold connected sum of $S^{2}\times S^{3}$ for all $k.$ Now, we show that LSE metrics exist on Smale manifolds for which $H_{2}(M,\mathbb{Z})_{tor}$ is nontrivial. 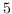In particular, we show that most simply-connected positive Sasakian rational homology $5$-spheres are also negative Sasakian (hence LSE). 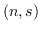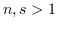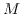Moreover, we show that for each pair of positive integers $(n,s)$ with $n,s >1$, there exists a Lorentzian Sasaki-Einstein Smale manifold $M$ such that $H_{2}(M,{\mathbb{Z}})_{tors}=(\mathbb{Z}/n)^{2s}$. 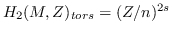Finally, we are able to construct so-called mixed Smale manifolds (connect sum of torsion free Smale manifolds with rational homology spheres) which admit LSE metrics and have arbitrary second Betti number. This gives infinitely many examples which do not admit positive Sasakian structures. These results partially address open problems formulated by C.Boyer and K.Galicki.

Key Words: Sasakian manifolds, Lorentzian-Einstien metrics, rational homology spheres.

2000 Mathematics Subject Classification: Primary: 53C25,
Secondary: 53D10, 53C50.