Abdul Hameed and Toru Nakahara: Integral bases and relative monogenity of pure octic fields, p.419-433

Abstract:

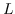
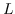
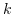
Let $m \ne 1$ be a square-free integer. The aim of this paper is to construct an integral basis of the pure octic field L=ℚ$\Q(\sqrt[8]{m})$ and to consider relative monogenity of $L$ over its quartic subfield K=ℚ(∜m) as well as over its quadratic subfield K=ℚ(√m). 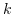We prove that the field $L$ is relatively monogenic over $k$ for the case of m ≡ 5,13 (mod 16) and does not have relative power integral basis over $k$ for m ≡ 1,9 (mod 16). 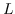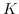Moreover we prove that $L$ has a relative power integral basis over $K$ in the case of m ≡ 5, 9, 13 (mod 16). 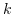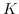We show that the field ℚ $\Q(\sqrt[8]{m})$ is monogenic as well as relatively monogenic over $k$ and $K$ when m ≡ 2, 3 (mod 4). 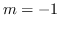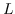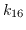In the case of $m = -1$ we prove our results by observing that the field $L$ coincides with the 16th cyclotomic field $k_{16}$.

Key Words: Pure octic field, integral basis, relative norm, power integral basis, monogenity.

2000 Mathematics Subject Classification: Primary: 11R04;
Secondary: 11R16, 11R21.

Download the paper in pdf format here.