Moharram Aghapournahr and Kamal Bahmanpour: Cofiniteness of weakly Laskerian local cohomology modules, p.347-356

Abstract:

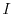
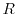
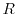
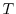
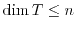
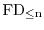
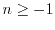
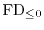
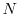
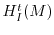
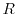
Let $I$ be an ideal of a Noetherian ring $R$ and M be a finitely generated $R$-module. We introduce the class of extension modules of finitely generated modules by the class of all modules $T$ with $\dim T\leq n$ and we denote it by ${\rm FD_{\leq n}}$ where $n\geq -1$ is an integer. 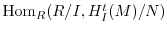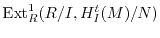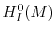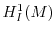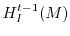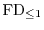We prove that for any ${\rm FD_{\leq 0}}$(or minimax) submodule $N$ of $H^t_I(M)$ the $R$-modules ${\rm Hom}_R(R/I,H^{t}_I(M)/N)$ and ${\rm Ext}^1_R(R/I,H^{t}_I(M)/N)$ are finitely generated, whenever the modules $H^0_I(M)$, $H^1_I(M)$, ..., $H^{t-1}_I(M)$ are ${\rm FD_{\leq 1}}$ ( or weakly Laskerian). 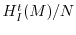As a consequence, it follows that the set of associated primes of $H^{t}_I(M)/N$ is finite. This generalizes the main results of Bahmanpour and Naghipour [4] and [5], Brodmann and Lashgari [6], Khashyarmanesh and Salarian [21] and Hong Quy [18]. 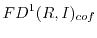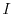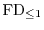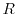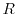We also show that the category $\mathscr {FD}^1(R,I)_{cof}$ of $I$-cofinite ${\rm FD_{\leq 1}}$  $R$-modules forms an Abelian subcategory of the category of all $R$-modules.

Key Words: Local cohomology module, cofinite module, Weakly Laskerian modules.

2000 Mathematics Subject Classification: Primary: 13D45;
Secondary: 14B15, 13E05.

Download the paper in pdf format here.