Susana-Clara López, Francisco Antonio Muntaner-Batle and Miquel Rius-Font: Perfect edge-magic graphs, p.81-91

Abstract:

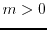
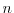
The study of the possible valences for edge-magic labelings of graphs has motivated us to introduce the concept of perfect edge-magic graphs. Intuitively speaking, an edge-magic graph is perfect edge-magic if all possible theoretical valences occur. 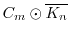In particular, we prove that for each integer $m>0$, that is the power of an odd prime, and for each natural number $n$, the crown product $C_m\odot \overline{K_n}$ is perfect edge-magic. Related results are also provided concerning other families of unicyclic graphs. Furthermore, several open questions that suggest interesting lines for future research are also proposed.

Key Words: Edge-magic, perfect edge-magic, valence.

2000 Mathematics Subject Classification: Primary: 05C78;
Secondary: 05C76.

Download the paper in pdf format here.