Let
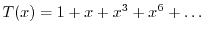
be the generating function of the Thue-Morse sequence. We show that for any coprime nonzero integers
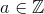
and
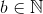
satisfying
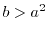
the irrationality exponent
of
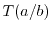
does not exceed
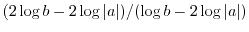
.
We also prove that infinitely many partial quotients of the number
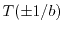
, where
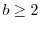
is an integer, lie in the set
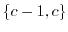
for some
integer
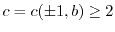
. For instance, the continued fraction of
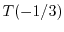
has infinitely many partial quotients smaller than or equal to
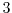
. In passing, we obtain the following Lagrange type result: if for an irrational number

whose continued fraction expansion has only finitely many partial quotients smaller than or equal to
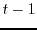
, where
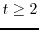
is an integer, and some coprime integers
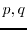
, where
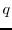
is large enough, we have
|α - p/q| < (t - 1)/tq2 then
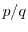
is a convergent to
α.