In this paper, a generalization of Lucas addition chains, where subtraction is allowed, is given. It is called ''Lucas addition-subtraction chain'' (LASC).
LASC gives minimal addition-subtraction chains for infinitely many integers and will also be used to prove the optimality of Lucas addition chains for many cases. One of the main result in the theory of addition-subtraction chains is due to Vogler [2] and this paper gives a way of getting addition-subtraction chains that satisfy his conditions.
Moreover, this paper will prove that Lucas addition chains give minimal addition chains for all even integers of Hamming weight
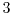
, like the
binary method. Finally, we give a theorem to get short (and many times minimal) Lucas addition-subtraction chains.