We survey results on holomorphic functions (of one complex variable) with values in a complex topological vector space hinting to their
extension to the case of several complex variables. We give a version of the Hartogs theorem on separate analyticity for
weakly holomorphic functions with values in a complex Fréchet space. The theory of
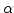
-differentiable functions
(due to N. Teodorescu, [27], and extended by F-H. Vasilescu, [28], to functions with values in a Fréchet space) is briefly
reviewed as related to areolar derivatives. We present a selection of results on holomorphic functions with values in a complex
Banach space with an emphasis on the boundary behavior of vector-valued holomorphic functions. We announce an extension of work by M.S. Baouendi & F. Treves, [3] (on the approximation of CR functions by holomorphic functions) to the case of CR functions with values in a complex
Fréchet space.
-differentiability, vector valued CR function.