D. Kuziak, I. Peterin, I. G. Yero: On the monopolies of lexicographic product graphs: bounds and closed formulas, p. 355-366

Abstract:

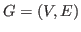
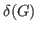
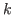
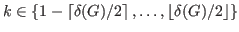
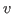
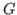
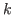
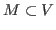
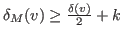
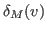
We consider a simple graph $G=(V, E)$ without isolated vertices and of minimum degree $\delta(G)$. Let $k$ be an integer number such that $k\in \left\{1-\left\lceil \delta(G)/2\right\rceil,\ldots,\left\lfloor \delta(G)/2\right\rfloor\right\}$. 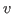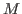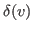A vertex $v$ of $G$ is said to be $k$-controlled by a set $M\subset V$, if $\delta_M(v)\ge \frac{\delta(v)}{2}+k$ where $\delta_M(v)$ represents the number of neighbors $v$ has in $M$ and $\delta(v)$ the degree of $v$. 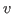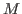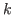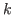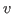The set $M$ is called a $k$-monopoly if it $k$-controls every vertex $v$ of $G$. 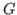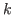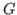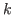The minimum cardinality of any $k$-monopoly in $G$ is the $k$-monopoly number of $G$. 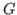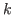In this article we study the $k$-monopolies of the lexicographic product of graphs. 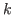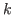Specifically we obtain several relationships between the $k$-monopoly number of this product graph and the $k$-monopoly numbers and/or order of its factors. 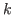Moreover, we bound (or compute the exact value) of the $k$-monopoly number of several families of lexicographic product graphs.

Key Words: monopolies; lexicographic product graphs

2010 Mathematics Subject Classification: Primary 05C69,
Secondary 05C76