Eugenie Hunsicker, Hengguang Li, Victor Nistor and Ville Uski: Analysis of Schrödinger operators with inverse square potentials I: regularity results in 3D, p.157-178

Abstract:

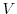
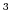
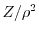
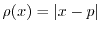
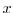
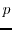
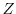
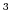
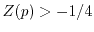
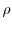
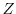
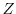
Let $V$ be a potential on ℜ$\RR^3$ that is smooth everywhere except at a discrete set S of points, where it has singularities of the form $Z/\rho^2$, with $\rho(x) = \vert x - p\vert$ for $x$ close to $p$ and $Z$ continuous on ℜ$\RR^3$ with $Z(p) > -1/4$ for p ∈ S. Also assume that $\rho$ and $Z$ are smooth outside S and $Z$ is smooth in polar coordinates around each singular point. 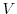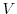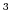We either assume that $V$ is periodic or that the set S is finite and $V$ extends to a smooth function on the radial compactification of ℜ$\RR^3$ that is bounded outside a compact set containing S. 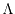In the periodic case, we let $\Lambda$ be the periodicity lattice and define T: = ℜ³/Λ. 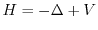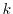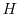We obtain regularity results in weighted Sobolev space for the eigenfunctions of the Schrödinger-type operator $H = -\Delta + V$ acting on L²(T), as well as for the induced $\vt k$-Hamiltonians H_k obtained by restricting the action of $H$ to Bloch waves. Under some additional assumptions, we extend these regularity and solvability results to the non-periodic case. We sketch some applications to approximation of eigenfunctions and eigenvalues that will be studied in more detail in a second paper.

Key Words: Regularity of eigenfunctions, Schrodinger operator, eigenvalue approximations, inverse square potential, regularity, weighted Sobolev spaces, rate of convergence of numerical methods, solid state physics.

2000 Mathematics Subject Classification: Primary: 35B65;
Secondary: 35J10, 65N12, 81Q05, 35B10, 35P10.

Download the paper in pdf format here.